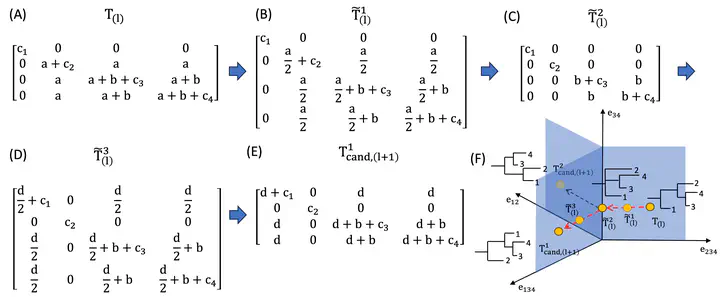
Abstract
Ultrametric matrices comprise a class of covariance matrices that arise in latent tree models. As a parameter space in a statistical model, the set of ultrametric matrices is neither convex nor a smooth manifold. Focus in the literature has hitherto been restricted to estimation through projections and relaxation-based techniques, and inferential methods are lacking. Motivated by this, we establish a bijection between the set of positive definite ultrametric matrices and the set of rooted, leaf-labeled trees equipped with the stratified geometry of the well-known phylogenetic treespace. Using the pullback geometry under the bijection and by adapting sampling techniques in Bayesian phylogenetics, we develop algorithms to sample from the posterior distribution on the set of ultrametric matrices in a Bayesian latent tree model where the tree may be binary or multifurcating. We demonstrate utility of the algorithms in simulation studies, and on a pre-clinical cancer application to quantify uncertainty about treatment trees that identify treatments with high mechanism similarity that target correlated pathways.