Bayesian Nonparametric Global-local Clustering of High-dimensional Functions

Abstract

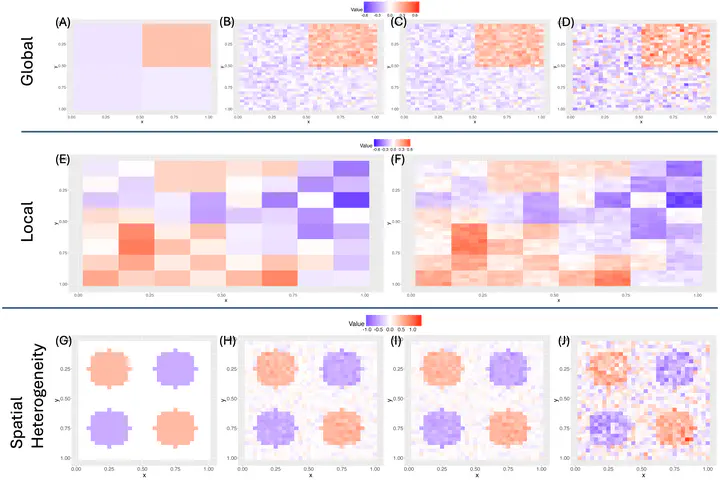
There is a rich literature on clustering functional data with applications to time-series modeling, trajectory data, and even spatio-temporal applications. Existing methods are classified into two categories of (i) global clustering that assigns an identical membership over the whole domain, and (ii) local clustering that allows multiple memberships based on the sub-domains. Classical literature has typically focused on global clustering that may struggle with degenerate clustering or produce numerous spurious clusters for high-dimensional functions. In contrast, a limited number of local clustering approaches have been proposed that are not scalable to high-dimensional functions and have limited theoretical guarantees. Focusing on basis expansions for high-dimensional functions, we propose a novel global-local framework that partitions coefficients into exclusive subsets and imposes independent Dirichlet process (DP) priors on each subset. The proposed framework reduces the total number of possible clustering configurations compared to local clustering and therefore provides greater scalability, while simultaneously providing enhanced flexibility compared to global clustering by relaxing the assumption of identical clustering for all elements in the high-dimensional function. Moreover, the proposed method incorporates spatially correlated errors to provide better model fitting and shows posterior consistency properties that asymptotically recover the true density of random functions. An efficient Markov chain Monte Carlo (MCMC) algorithm is developed for implementation. Extensive simulations involving images illustrate the improved scalability, clustering, and function estimation under the proposed method compared to classical approaches. We apply the proposed approach to a spatial transcriptomics application where the goal is to infer clusters of genes with distinct spatial patterns of expressions. Our method makes an important contribution to the limited literature on clustering methods for high-dimensional functions with important applications to imaging data and beyond.